思考三角函数 余弦定理的时候想到了勾股定理 从而得到了
$$
{sin^2x + cos^2x = 1}
$$
这么一条公式 尽管这并不是余弦定理的支撑 但勾股定理是如何证明的

然后翻看资料发现 勾股定理是余弦定理的一种特殊情况 而正弦定理同样独立于勾股定理 且正弦定理给出了三角形边与角及外接圆的关系 这正好解决了我的一些疑问

抽象来看 也就是从给定值出发 去寻找我们目标之外的确定数学关系 从该关系去演化和构造

那么勾股定理不属于平面公理 则应当从某些公式推到演变出来

我们注意到这种证明方式

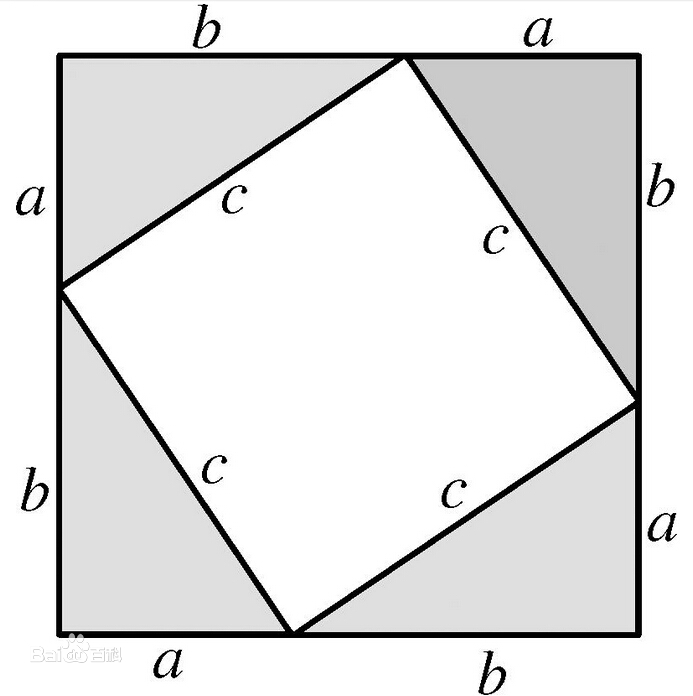
非常巧妙 其本质 当我们证明对应c的关系时 我们去构造单独以ab为元素 并由平面构造出对c的计算 这里引出了一个面积计算公式 以及两个角度的问题 x+y+90=180 而180为直线 剩余的90°角作为正方形的角 当然这都是很基础的一些定义

但是为什么由这些基础能够推算出勾股定理 我们又如何能够构造出这样的图形 我们再看另一个

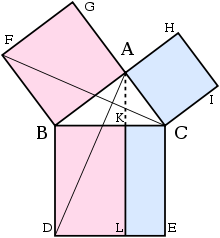
这里有一点是三角形的相似性 是上面没有用到的 简单的通过相似性 把BC用AC AB替换掉 从而去做到一个对 $c^2$的计算 而这种关联本身是存在于一种未知的比例 也就是$\frac{AC}{BC}$ 和$\frac{KC}{AC}$ 这两个比例是相等的 但是却是未知的 这时候我们应该理解 这里是三个变量存在一种关联 从而实现将其中一个变量用另外两个变量替换

那么我们可以合理外推 若 具体事件 = 3未知+1已知 则有 1未知=2未知

合理外推为 若 具体事件 = N未知+M已知 则有 M未知 = (N-M)未知

那么在这个时候 由于存在三角形的相似性 我们得到 BC AC CK三个未知条件 $\frac{BC}{AC} = \frac{AC}{CK}$ 这样一个已知条件 从而得到实现 1未知=2未知

那么问题在于 BC CK都是属于BC的线段 我们应该把三个未知条件的哪个拿出来放在等式左边？

我们注意到 BC · CK实际上就是下方KLEC的面积 这时候又有了新的问题 如何将数论与平面几何结合在一起

抛开这些图形不看 当我们看到这样一个公式 $a^2 + b^2 = c^2$时 如何去构思证明 首先我们要明白这是一个几何学问题 是为了探寻几何图形的性质 我们需要使用数论和已知的几何性质去进行推演

在数论中有一些方法 去把整个公式做一些变换 在这里比较贴切的是 平方和/差公式 即拆分成$c^2 = (a+b)^2-2ab$ 或者 $b^2 = (c-a)^2+ 2ac$